MySQL Indexing for Performance

I just learned about indexing on a MySQL database at a fairly high-level and will attempt to summarize what I’ve learned. MySQL has many different kinds of indexes (full-text indexes, spatial indexes, TokuDB - fractal tree index, ScaleDB - Patricia Trie, InfiniDB - special logic) but for most use cases, InnoDB and MyISAM are the two most common.

Until MySQL 5.5, the default index was MyISAM. MyISAM is good for analytical use cases because it has table-level locking which means two users cannot query the same table at the same time. Because of this, MyISAM can get away with not being ACID compliant as well as non-transactional. Furthermore, MyISAM doesn’t support relational contraints like Foreign Keys which means that it is better to have wider tables in MyISAM rather than a First Normal Form database.

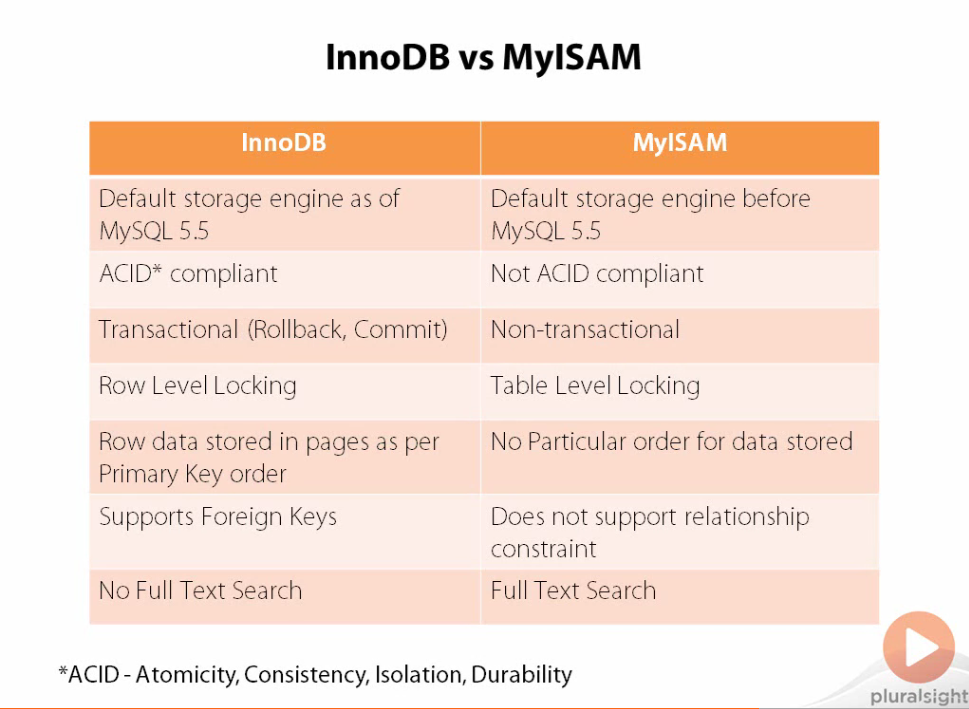
Both InnoDB and MyISAM leverage B-tree data structures to improve query speeds. In a B-tree index, values are stored in order and each leaf is at the same distance from the root level. However, MyISAM and InnoDB again differ in that MyISAM stores keys and data in internal nodes whereas InnoDB only stores data in its leaf nodes with the internal nodes only containing pointers to their children. We call the InnoDB version of B-tree a B+tree to differentiate it from the one used in MyISAM. Due to the fact that data is only stored in the leaf nodes, InnoDB can store more indexes in memory as it traverses the tree and is therefore much smaller than a B-tree.

But you may be wondering, “Why B-trees?” B-trees are used because it speeds up data access. Storage engines are able to traverse the tree from the root node to the leaf node with the help of pointers even though the locations of these nodes might be spread out in the computer’s memory. We also see increased performance for full value (“Kyle Schmidt”), leftmost value or column prefix (“Kyle” from “Kyle Schmidt”), and range of values (1 to 99) query patterns as well as aiding our ORDER BY clauses because nodes point to each other in order (more to come).

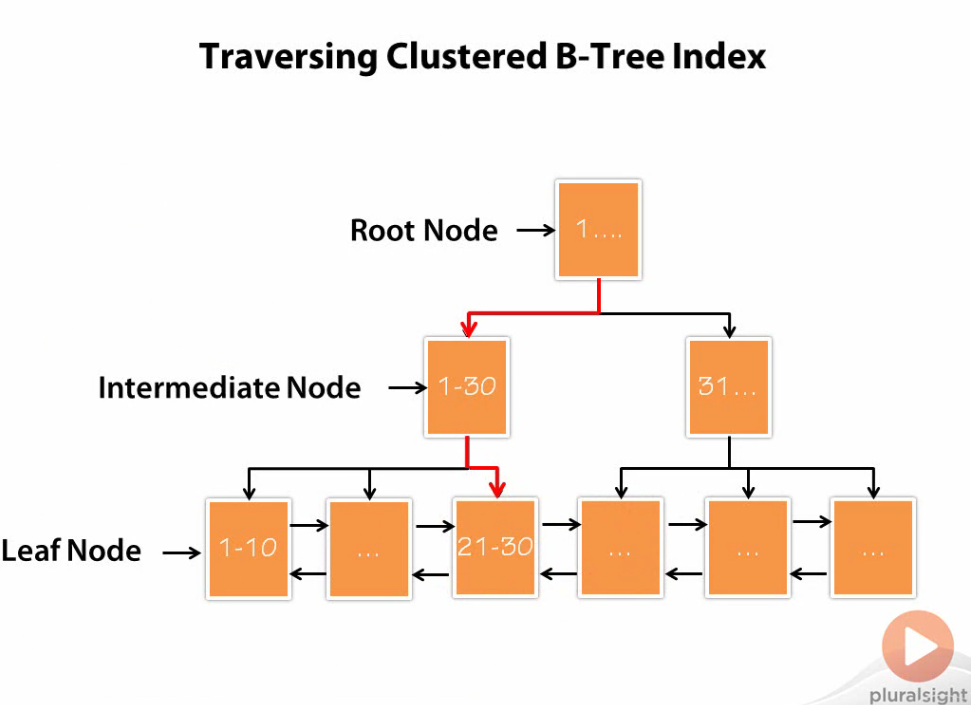
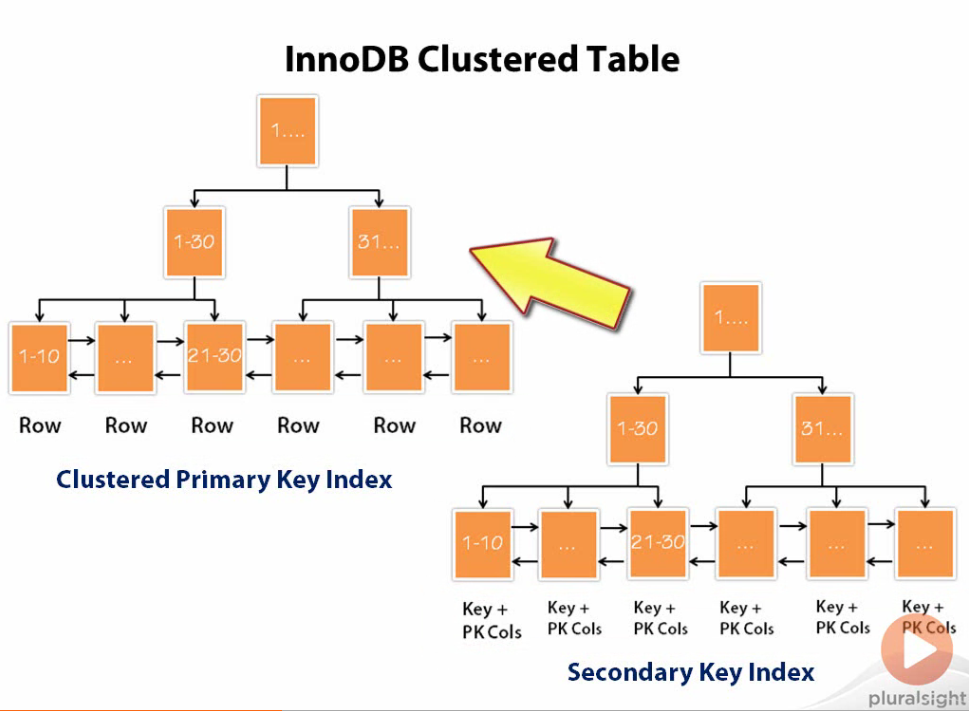
Sometimes a single node representing a key still doesn’t offer the efficiency that we need. What if we want to store keys that are close in proximity such as employees of a certain profession? This is where cluster indexes come in to play. We will use cluster indexes throughout the rest of this article to talk about B-trees. Cluster indexes have the same structure as B-trees but each “node” of a cluster B-tree contains a cluster of keys rather than a single key.

The advantages of cluster indexes are that related data is stored close to each other leading to less disk I/O while retrieving sequential or range data rather than performing a full table scan for indexes that are similar. Furthermore, cluster indexes allow even further optimizations for data retrieval since data and indexes are stored together at leaf nodes. Lastly, leaf nodes point to each other. Thereby, if you perform a query on a range of data that is held within two internal cluster nodes of the cluster B-tree (in the simplest case) then the leaf nodes will be able to point to the next cluster in order without having to backtrack up the tree.

The disadvantages of a cluster index are that data insertion speed is dependent on the order of the primary key. The table needs to be re-indexed/optimized if inserted data is not ordered by primary key which could potentially take quite a long time - time that your application might not afford to spend. Clusters can split when new data is inserted which can lead to fragmentation of the cluster indexed B-tree structure. All of these contribute to poor performance if the cluster index isn’t re-optimized when performing an ill-adviced insertion.

B-trees support secondary indexes which further aid our queries. All tables should have multiple secondary indexes aside from primary indexes in order to aid query optimization. In InnoDB, the secondary index does not store actual data but only contains a pointer to the row of data. However, if the secondary index is coupled with a primary index then the secondary index will contain a pointer to the primary index. Secondary indexes are necessary because our queries usally make use of multiple columns of a single SQL table and therefore a single primary index will not suffice. For example, our first query could be on a column labeled first_name and a second query on a column labeled last_name. We would need two different indexes over both of these columns in order to optimize these queries. To carry-out our example with last_name being our secondary index and first_name as our primary index, the last_name index will point to the index for its corresponding first_name which will contain the data that it represents. Similarly, a last_name only query will require the secondary key index to find the appropriate last_name and then the pointer will jump back to the primary key index before data retrieval.

Yet, there is one last type optimization that I want to talk about, Hash Indexes. Hash indexes are built on top of hash tables and increase query performance for exact lookups. You can think of a hash as a function that when given an input computes the key of a map or dictionary-like data structure. Hash indexes work by creating a hash value or key for each row of data. Given an exact match of that row of data, the hash table will compute the hash of that match which ‘salts’ to the index of a hash table pointing to its representative row of data. Generally, different keys generate different hash codes but if multiple values have the same hash code, then the value of the hash code in the hash table will be a linked list of row pointers. Hash indexes are even faster than B-trees when a key doesn’t contain a linked list and effective since the table resides in memory.

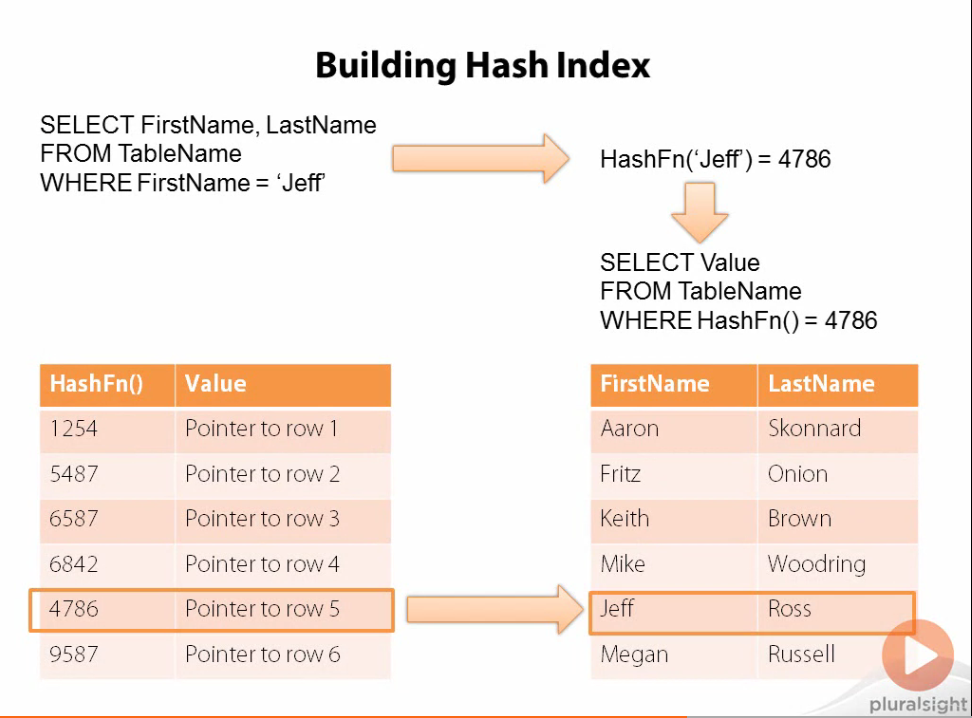
However, there are limitations to Hash indexes. Hash indexes only contains the hash code and pointers to a row of data, not the data itself. Because it doesn’t contain the original data, hash indexes are not suitable for sorting or partial matching - it can only support the equal operator. Furthermore, I also mentioned that it is possible for multiple rows to have the same hash code, creating a linked list. This will slow down query time considerably in these cases, creating a linear seach for a node row pointer.

But what if there is a way to leverage both the efficiency of B-trees and Hash indexes? This is exactly what InnoDB does. It uses what is called an Adaptive Hash Index which sits on top of a B+tree. This comes “out-of-the-box” when you use InnoDB indexing with the caveat thast it can’t be modified of configured. The Adaptive Hash Index works by evaluating a query for its Hash Index _and_the B+tree Index, allowing us to leverage the quick lookup of hash tables and the traversal of relative nodes in a B+tree.

Slides provided by Pluralsight.com